| Classwise Concept with Examples | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 11 Constructions (Concepts)
Welcome to this chapter dedicated to the art and science of Geometric Constructions. Building upon the foundational construction skills acquired in earlier classes, this section emphasizes not only the 'how' but, more critically, the 'why' behind each construction. We move into a realm where precision is paramount, and every construction must be performed using only two fundamental tools: an unmarked ruler (or straightedge) and a pair of compasses. This classical approach forces us to rely entirely on pure geometric principles rather than measurement tools like protractors (except perhaps for verification). The cornerstone of this chapter is the requirement for rigorous mathematical justification for each construction performed, ensuring a deep understanding of the underlying geometry.
We begin by revisiting and refining fundamental constructions that serve as building blocks for more complex figures. These include:
- Bisecting a given angle: Accurately constructing the ray that divides a given angle into two angles of equal measure. The justification relies on proving the congruence of triangles formed during the construction (typically using SSS).
- Constructing the perpendicular bisector of a given line segment: Creating the line that intersects the segment at its midpoint and is perpendicular to it. The justification hinges on properties of rhombuses or congruent triangles (SSS or SAS).
Following these basics, we focus on constructing angles of specific measures without using a protractor. This relies on leveraging fundamental geometric shapes and angle properties:
- A $60^\circ$ angle is fundamental, derived from constructing an equilateral triangle.
- A $90^\circ$ angle can be constructed by bisecting a straight angle ($180^\circ$) or constructing a perpendicular at a point on a line.
- Other angles are then derived through bisection or combination:
- $45^\circ$ by bisecting $90^\circ$.
- $30^\circ$ by bisecting $60^\circ$.
- $22.5^\circ$ (or $22\frac{1}{2}^\circ$) by bisecting $45^\circ$.
- $75^\circ$ as $60^\circ + 15^\circ$ (where $15^\circ$ is half of $30^\circ$) or $90^\circ - 15^\circ$.
- $105^\circ$ as $60^\circ + 45^\circ$ or $90^\circ + 15^\circ$.
- $135^\circ$ as $90^\circ + 45^\circ$.
The justification for each involves explaining the sequence of basic constructions (equilateral triangle, perpendiculars, bisections) used.
The major focus, however, shifts to constructing triangles under conditions that go beyond the basic SSS, SAS, and ASA criteria learned previously. These more intricate constructions require clever application of geometric properties:
- Constructing a triangle given its base, one base angle, and the sum of the lengths of the other two sides. This involves using the properties of isosceles triangles and perpendicular bisectors.
- Constructing a triangle given its base, one base angle, and the difference between the lengths of the other two sides. This construction has two possible cases, depending on which of the two sides is longer, and again relies on careful use of arcs and perpendicular bisectors.
- Constructing a triangle given its perimeter (sum of all three sides) and its two base angles. This complex construction involves creating angles equal to half the base angles at the ends of a segment equal to the perimeter.
For every construction performed in this chapter, simply following the steps is insufficient. The critical requirement is to provide a clear, logical justification (a proof) demonstrating *why* the resulting figure satisfies all the given conditions. These justifications typically rely heavily on proving triangle congruence (using SSS, SAS, ASA, RHS criteria) and applying known properties of isosceles triangles, angle bisectors, and perpendicular bisectors. This rigorous approach bridges the gap between practical drawing and theoretical geometry, enhancing not only precision and technical skill but also fostering deep logical thinking and reinforcing the interconnectedness of geometric concepts.
Construction of Perpendicular Bisector and its Justification
In the realm of geometry, a construction refers to the process of drawing geometric shapes and figures using only a compass and a straightedge (which is an unmarked ruler). These tools are fundamental in Euclidean geometry. One of the essential constructions is creating the perpendicular bisector of a line segment. A perpendicular bisector of a line segment is a line that intersects the segment at its exact midpoint and forms a right angle ($90^\circ$) with the segment.
Construction: To construct the perpendicular bisector of a given line segment.
The perpendicular bisector of a line segment is a line that divides the segment into two equal parts at a right angle (90°). Every point on the perpendicular bisector is equidistant from the two endpoints of the line segment.
General Steps of Construction:
Let AB be the given line segment that we need to bisect perpendicularly.
- With point A as the centre, open the compass to a radius that is more than half the length of AB. Draw two arcs, one above the line segment AB and one below the line segment AB.
- Now, with point B as the centre and using the same radius as used in Step 1, draw two other arcs. Ensure these arcs intersect the previously drawn arcs. Let the points where these arcs intersect be P and Q.
- Draw a straight line passing through the intersection points P and Q. This line is the required perpendicular bisector of AB.
Example. Draw a line segment of length 7.6 cm and construct its perpendicular bisector.
Answer:
Given:
A line segment AB of length 7.6 cm.
To Construct:
The perpendicular bisector of the line segment AB.
Steps of Construction:
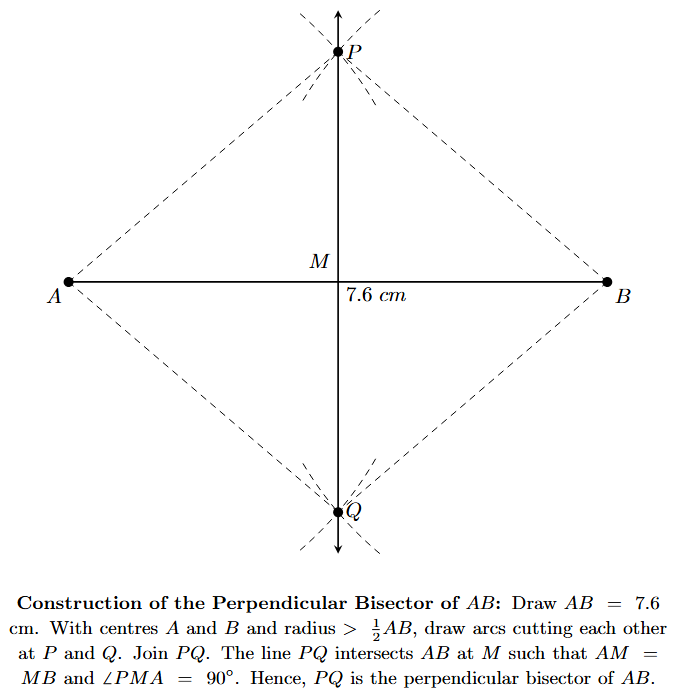
Step 1: Draw a line segment AB of length 7.6 cm using a ruler.

Step 2: With A as the centre and taking a radius more than half of AB (e.g., 5 cm), draw two arcs, one above and one below the line segment AB.

Step 3: With B as the centre and using the same radius (5 cm), draw two more arcs that intersect the arcs drawn in the previous step. Mark the points of intersection as P and Q.
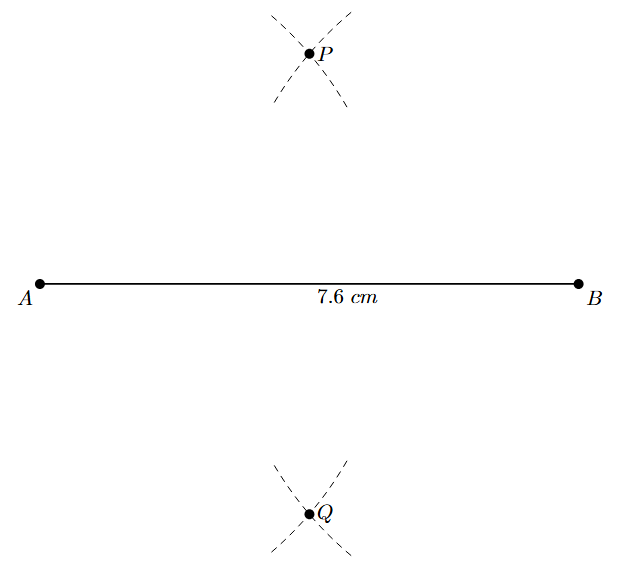
Step 4: Join the points P and Q using a ruler. The line PQ intersects the line segment AB at a point M. The line PQ is the required perpendicular bisector of AB.
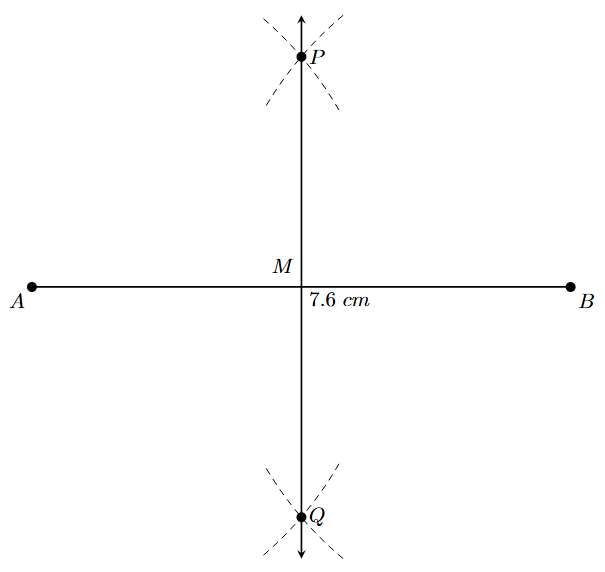
By measurement, we can verify that AM = MB = 3.8 cm and $\angle$PMA = 90°.
Justification of Construction:
We need to prove that the constructed line PQ is indeed the perpendicular bisector of the line segment AB. This means we must prove two things:
(i) PQ bisects AB (i.e., AM = BM).
(ii) PQ is perpendicular to AB (i.e., $\angle \text{PMA} = 90^\circ$).
Given:
A line segment AB. Points P and Q are located such that they are equidistant from A and B.
To Prove:
(i) AM = BM
(ii) $\text{PQ} \perp \text{AB}$
Proof:
First, we consider $\triangle \text{PAQ}$ and $\triangle \text{PBQ}$.
PA = PB
(Arcs of equal radii)
QA = QB
(Arcs of equal radii)
PQ = PQ
(Common side)
Therefore, by the Side-Side-Side (SSS) congruence criterion:
$\triangle \text{PAQ} \cong \triangle \text{PBQ}$
(SSS Rule)
Since the triangles are congruent, their corresponding parts are equal. Thus,
$\angle \text{APQ} = \angle \text{BPQ}$
(CPCTC) ... (i)
Now, we consider $\triangle \text{PAM}$ and $\triangle \text{PBM}$.
PA = PB
(Arcs of equal radii)
$\angle \text{APM} = \angle \text{BPM}$
(From (i), as M lies on PQ)
PM = PM
(Common side)
Therefore, by the Side-Angle-Side (SAS) congruence criterion:
$\triangle \text{PAM} \cong \triangle \text{PBM}$
(SAS Rule)
Since the triangles are congruent, their corresponding parts must be equal.
AM = BM
(CPCTC)
This proves that the line PQ bisects the line segment AB.
Also, by CPCTC:
$\angle \text{PMA} = \angle \text{PMB}$
(CPCTC) ... (ii)
Since AB is a straight line, the angles $\angle \text{PMA}$ and $\angle \text{PMB}$ form a linear pair.
$\angle \text{PMA} + \angle \text{PMB} = 180^\circ$
(Linear Pair Axiom)
Substituting $\angle \text{PMA}$ for $\angle \text{PMB}$ using equation (ii):
$\angle \text{PMA} + \angle \text{PMA} = 180^\circ$
$2 \angle \text{PMA} = 180^\circ$
$\angle \text{PMA} = \frac{180^\circ}{2} = 90^\circ$
This proves that $\text{PQ} \perp \text{AB}$.
Since PQ bisects AB and is also perpendicular to it, PQ is the perpendicular bisector of AB. Hence, the construction is justified.
Construction of Angle Bisector and its Justification
An angle bisector is a ray that originates from the vertex of an angle and divides the angle into two angles of equal measure. Constructing an angle bisector using only a compass and straightedge is a fundamental construction in geometry.
Construction: To construct the bisector of a given angle.
The angle bisector is a ray that divides a given angle into two angles of equal measure. Every point on the angle bisector is equidistant from the two arms of the angle.
General Steps of Construction:
Let $\angle \text{BAC}$ be the given angle that we want to bisect.
- With A as the centre, draw an arc with any convenient radius such that it intersects both arms AB and AC of the angle. Let the points of intersection be P on AB and Q on AC.
- Now, with P as the centre, open the compass to a radius that is greater than half the length of the chord PQ. Draw an arc in the interior of $\angle \text{BAC}$.
- With Q as the centre and using the same radius as used in the previous step, draw another arc in the interior of $\angle \text{BAC}$. This arc should intersect the arc drawn previously. Let the point of intersection of these two arcs be R.
- Draw a ray starting from the vertex A and passing through the point R. This ray AR is the bisector of the given angle $\angle \text{BAC}$.
Example. Construct an angle of 70° using a protractor and construct its bisector using a compass and ruler.
Answer:
Given:
An angle, say $\angle \text{BAC}$, of measure 70°.
To Construct:
The bisector of $\angle \text{BAC}$.
Steps of Construction:
Step 1: Draw a ray AB. Using a protractor, construct $\angle \text{BAC} = 70^\circ$.
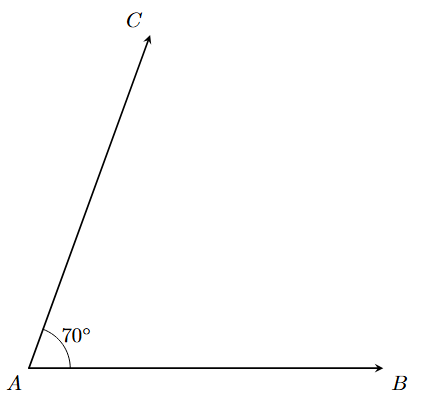
Step 2: With A as the centre and any convenient radius, draw an arc that intersects the arms AB and AC at points P and Q, respectively.
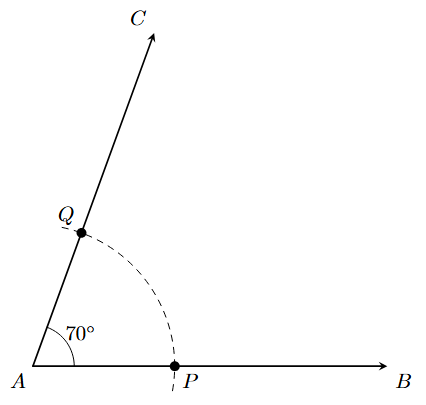
Step 3: With P as the centre and a radius greater than half of PQ, draw an arc in the interior of the angle.

Step 4: With Q as the centre and the same radius as in the previous step, draw another arc that intersects the first arc at a point, say R.

Step 5: Join the points A and R and extend it to form a ray. The ray AR is the required bisector of $\angle \text{BAC}$.

On measuring, we can verify that $\angle \text{BAR} = \angle \text{CAR} = 35^\circ$.
Justification of Construction:
We need to justify why the ray AR is the angle bisector of $\angle \text{BAC}$. This means we need to prove that ray AR divides the angle into two equal angles, i.e., $\angle \text{BAR} = \angle \text{CAR}$.
Given:
An angle $\angle \text{BAC}$ and a constructed ray AR.

To Prove:
Ray AR bisects $\angle \text{BAC}$, i.e., $\angle \text{BAR} = \angle \text{CAR}$.
Construction:
Join PR and QR.
Proof:
In $\triangle \text{APR}$ and $\triangle \text{AQR}$,
AP = AQ
(Radii of the same arc)
PR = QR
(Arcs of equal radii)
AR = AR
(Common side)
Therefore, by the Side-Side-Side (SSS) congruence criterion:
$\triangle \text{APR} \cong \triangle \text{AQR}$
(SSS Rule)
Since the triangles are congruent, their corresponding parts are equal.
$\angle \text{PAR} = \angle \text{QAR}$
(CPCTC)
This is the same as:
$\angle \text{BAR} = \angle \text{CAR}$
Thus, the ray AR bisects $\angle \text{BAC}$. Hence, the construction is justified.
Construction of Equilateral Triangle and its Justification
An equilateral triangle is a polygon with three sides of equal length and three equal angles ($60^\circ$ each). Constructing an equilateral triangle is one of the most basic constructions using a compass and straightedge, relying directly on the definition of a circle.
Construction: To construct an equilateral triangle of a given side length.
An equilateral triangle is a triangle in which all three sides have the same length. Consequently, all three angles are also equal, each measuring 60°.
General Steps of Construction:
- Draw a line segment which will be the base of the triangle, with the given length.
- With one endpoint of the segment as the centre, draw an arc with a radius equal to the side length.
- With the other endpoint as the centre and the same radius, draw another arc that intersects the first arc.
- The point of intersection is the third vertex of the triangle. Join this point to the two endpoints of the base segment.
Example. Construct an equilateral triangle of side 5 cm.
Answer:
Given:
The length of the side of the equilateral triangle is 5 cm.
To Construct:
An equilateral triangle ABC with side length 5 cm.
Steps of Construction:
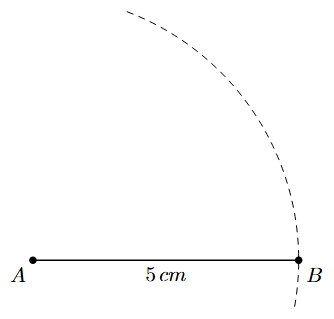
Step 1: Draw a line segment AB of length 5 cm using a ruler.

Step 2: With A as the centre and a radius of 5 cm, draw an arc.
Step 3: With B as the centre and the same radius of 5 cm, draw another arc to intersect the arc from Step 2. Mark the point of intersection as C.
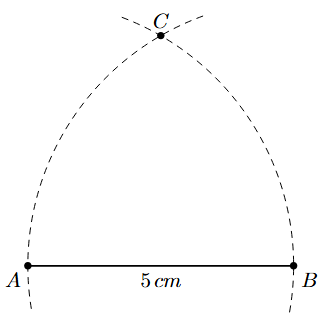
Step 4: Join AC and BC. The triangle ABC is the required equilateral triangle.

Justification of Construction:
We need to justify why the triangle ABC constructed is an equilateral triangle. This requires proving that all three sides are equal.
Given:
A triangle ABC constructed as per the steps above.

To Prove:
$\triangle \text{ABC}$ is an equilateral triangle (i.e., $\text{AB} = \text{BC} = \text{AC}$).
Proof:
By construction, we drew a line segment AB of length 5 cm.
$\text{AB} = 5 \text{ cm}$
(By construction) ... (i)
From point A, we drew an arc of radius 5 cm. Point C lies on this arc.
$\text{AC} = 5 \text{ cm}$
(Radius of the arc from A) ... (ii)
From point B, we drew an arc of radius 5 cm. Point C also lies on this arc.
$\text{BC} = 5 \text{ cm}$
(Radius of the arc from B) ... (iii)
From equations (i), (ii), and (iii), we have:
$\text{AB} = \text{BC} = \text{AC} = 5 \text{ cm}$
Since all three sides of $\triangle \text{ABC}$ are equal, it is an equilateral triangle. This justifies the construction.
Construction of Standard Angles
The construction of an equilateral triangle is the basis for constructing a $60^\circ$ angle, which in turn allows us to construct many other standard angles using a compass and ruler.
Constructing a $60^\circ$ angle:
- Draw a ray AB.
- With A as centre, draw an arc of any radius intersecting AB at point X.
- With X as centre and the same radius, draw an arc intersecting the first arc at point C.
- Draw the ray AC. The angle $\angle \text{CAB}$ is $60^\circ$.
Justification: By construction, $\text{AX} = \text{AC} = \text{XC}$ (all are equal to the chosen radius). Thus, $\triangle \text{AXC}$ is an equilateral triangle. Since all angles in an equilateral triangle are $60^\circ$, it follows that $\angle \text{CAB} = 60^\circ$.
Constructing a $30^\circ$ angle:
- Construct a $60^\circ$ angle $\angle \text{CAB}$ as described above.
- Bisect the angle $\angle \text{CAB}$ using the angle bisector construction. Let AR be the bisector.
- The angle $\angle \text{RAB}$ is $30^\circ$.
Justification: The ray AR bisects the $60^\circ$ angle into two equal parts. Therefore, $\angle \text{RAB} = \frac{60^\circ}{2} = 30^\circ$.
Constructing a $120^\circ$ angle:
- Draw a ray AB.
- With A as centre, draw a large arc of any radius intersecting ray AB at X.
- With X as centre and the same radius, draw an arc intersecting the first arc at Y.
- With Y as centre and the same radius, draw another arc intersecting the large arc at Z.
- Draw the ray AZ. The angle $\angle \text{ZAB}$ is $120^\circ$.
Justification: By construction, $\triangle \text{AXY}$ is equilateral, so $\angle \text{YAX} = 60^\circ$. Similarly, $\triangle \text{AYZ}$ is equilateral, so $\angle \text{ZAY} = 60^\circ$. The total angle is $\angle \text{ZAB} = \angle \text{YAX} + \angle \text{ZAY} = 60^\circ + 60^\circ = 120^\circ$.
Constructing a $90^\circ$ angle (Perpendicular):
- Draw a ray AB.
- Construct a $60^\circ$ angle (point Y on the arc) and a $120^\circ$ angle (point Z on the arc) as described above.
- The angle between the $60^\circ$ mark (Y) and the $120^\circ$ mark (Z) is $60^\circ$. Now, bisect this $60^\circ$ angle $\angle \text{ZAY}$.
- With Y and Z as centres, and a radius greater than half of YZ, draw two arcs that intersect at a point R.
- Draw the ray AR. The angle $\angle \text{RAB}$ is $90^\circ$.
Justification: The ray AR is the bisector of $\angle \text{ZAY}$. So, $\angle \text{RAY} = \frac{60^\circ}{2} = 30^\circ$. The total angle is $\angle \text{RAB} = \angle \text{YAB} + \angle \text{RAY} = 60^\circ + 30^\circ = 90^\circ$.
Construction of other angles ($45^\circ$, $15^\circ$, $75^\circ$, $105^\circ$):
These angles are constructed by repeatedly bisecting the angles constructed above.
- $45^\circ$: Construct a $90^\circ$ angle and then bisect it. ($45^\circ = \frac{90^\circ}{2}$).
- $15^\circ$: Construct a $60^\circ$ angle, bisect it to get $30^\circ$, and then bisect the $30^\circ$ angle. ($15^\circ = \frac{30^\circ}{2}$).
- $75^\circ$: This is the sum of $60^\circ$ and $15^\circ$. Construct a $90^\circ$ angle and a $60^\circ$ angle on the same base ray. The angle between them is $30^\circ$. Bisect this $30^\circ$ angle to get $15^\circ$. The angle between the base ray and this bisector is $60^\circ + 15^\circ = 75^\circ$.
- $105^\circ$: This is the sum of $90^\circ$ and $15^\circ$. Construct a $90^\circ$ angle and a $120^\circ$ angle on the same base ray. The angle between them is $30^\circ$. Bisect this $30^\circ$ angle to get $15^\circ$. The angle between the base ray and this bisector is $90^\circ + 15^\circ = 105^\circ$.
Construction of a Triangle when Two Sides and Median is Given
In this construction, we are given the lengths of two sides of a triangle and the length of the median to the third side. We need to construct the triangle using a compass and straightedge.
Let the given lengths of the two sides be $c$ and $b$, and the length of the median to the third side be $m_a$. We want to construct $\triangle \text{ABC}$, where AB = $c$, AC = $b$, and AD is the median to BC with AD = $m_a$ (D is the midpoint of BC).
Construction: To construct a triangle given two sides and the median to the third side.
A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side. This construction is not straightforward, so we use a clever method that involves constructing a parallelogram related to the desired triangle. The key property used is that the diagonals of a parallelogram bisect each other.
Example. Construct a triangle ABC in which AB = 5 cm, AC = 6 cm, and the median AD = 4 cm.
Answer:
Given:
- Side AB = 5 cm.
- Side AC = 6 cm.
- Median AD = 4 cm (where D is the midpoint of BC).
To Construct:
A triangle ABC with the given measurements.
Analysis and Steps of Construction:
We will construct a parallelogram ABEC where AE and BC are the diagonals intersecting at D. In this parallelogram, we will have BE = AC. We can first construct the triangle ABE for which we know all three sides: AB = 5 cm, AE = 2 × AD = 8 cm, and BE = AC = 6 cm.
Step 1: Draw a line segment AD of length 4 cm.

Step 2: Extend the line segment AD to a point E such that AD = DE. So, DE = 4 cm and the total length AE = 8 cm.

Step 3: With A as the centre, draw an arc with a radius of 5 cm (the length of side AB).

Step 4: With E as the centre, draw an arc with a radius of 6 cm (the length of side AC, which will be equal to BE). This arc should intersect the arc from Step 3. Mark the point of intersection as B.

Step 5: Join AB and EB. This completes the triangle ABE.

Step 6: Join B and D and extend the line segment. Since D is the midpoint of BC, we need to find C such that BD = DC. Measure the length of BD with a compass, and with D as the centre, cut an arc on the extended line BD. Mark this point as C.
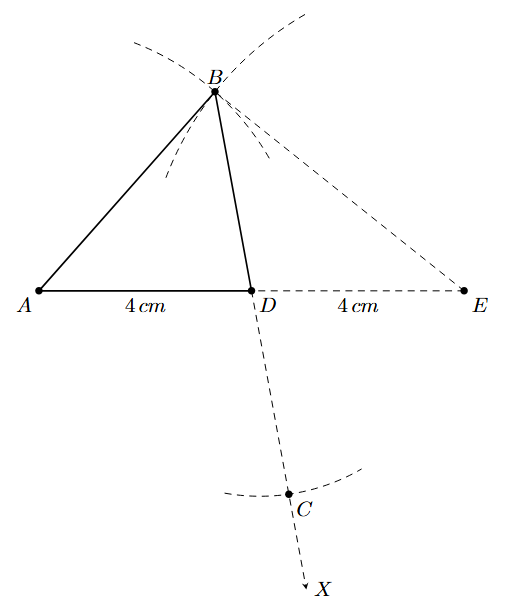
Step 7: Join A to C. The triangle ABC is the required triangle.

Justification:
We need to justify that the constructed triangle ABC has the given side lengths AB=5 cm and AC=6 cm, and that AD=4 cm is the median to side BC.
To Prove:
In the final figure $\triangle \text{ABC}$, AB = 5 cm, AC = 6 cm, and AD is the median to BC with length 4 cm.
Proof:

In the quadrilateral ABEC, consider the diagonals AE and BC.
By construction (Step 2), we have AD = DE, which means D is the midpoint of AE.
By construction (Step 6), we have BD = DC, which means D is the midpoint of BC.
Since the diagonals AE and BC bisect each other at point D, the quadrilateral ABEC is a parallelogram.
In a parallelogram, opposite sides are equal. Therefore,
AC = BE
(Opposite sides of a parallelogram)
Now, let's review our construction steps:
AB = 5 cm
(By construction, Step 3)
AD = 4 cm
(By construction, Step 1)
BE = 6 cm
(By construction, Step 4)
Since AC = BE, we have:
AC = 6 cm
Also, since D is the midpoint of BC (by Step 6), AD is the median to the side BC in $\triangle \text{ABC}$.
Thus, we have successfully constructed a triangle ABC with side AB = 5 cm, side AC = 6 cm, and median AD = 4 cm. This justifies the construction.
Construction of a Triangle when Two angles and Altitude is Given
In this construction, we are given the measures of two angles of a triangle and the length of the altitude from the third vertex to the side opposite to it. We need to construct the triangle using a compass and straightedge.
Let the given angles be $\angle \text{B}$ and $\angle \text{C}$, and the length of the altitude from vertex A to side BC be $h_a$. We need to construct $\triangle \text{ABC}$ such that $\angle \text{ABC} = \angle \text{B}$, $\angle \text{ACB} = \angle \text{C}$, and the altitude AD from A to BC has length $h_a$ (where D lies on the line containing BC and $\text{AD} \perp \text{BC}$).
Note: For a triangle to be constructible, the sum of the two given angles must be less than $180^\circ$ ($\angle \text{B} + \angle \text{C} < 180^\circ$). If $\angle \text{B} + \angle \text{C} = 180^\circ$, the lines forming the triangle would be parallel. If $\angle \text{B} + \angle \text{C} > 180^\circ$, it's impossible in Euclidean geometry.
Construction: To construct a triangle given two base angles and the altitude from the third vertex.
This construction involves creating the altitude first and then using the properties of right-angled triangles to determine the base vertices. If we have a triangle ABC with altitude AD, we have two right-angled triangles, $\triangle$ADB and $\triangle$ADC. The sum of angles in a triangle is 180°, so in $\triangle$ADB, we know $\angle$B, $\angle$ADB = 90°, and therefore we can find $\angle$BAD = 90° - $\angle$B. Similarly, in $\triangle$ADC, $\angle$CAD = 90° - $\angle$C. We will use this relationship to construct the triangle.
General Steps of Construction:
- Draw a long reference line, which will contain the base of the triangle. Mark a point D on it.
- Construct a line perpendicular to the reference line at point D.
- On this perpendicular line, mark the vertex A at a distance equal to the given altitude from D.
- From vertex A, construct an angle equal to (90° - $\angle$B) on one side of the altitude. The ray of this angle will intersect the reference line at vertex B.
- From vertex A, construct an angle equal to (90° - $\angle$C) on the other side of the altitude. The ray of this angle will intersect the reference line at vertex C.
- Join the vertices to form the required triangle ABC.
Example. Construct a triangle ABC in which the base angles are $\angle$B = 60° and $\angle$C = 45°, and the altitude from vertex A to the base BC is AD = 4.5 cm.
Answer:
Given:
- Base angle $\angle$B = 60°.
- Base angle $\angle$C = 45°.
- Altitude AD = 4.5 cm.
To Construct:
A triangle ABC with the given measurements.
Analysis:
We will construct angles at vertex A relative to the altitude AD.
In the right-angled $\triangle$ADB, $\angle$BAD = 90° - $\angle$B = 90° - 60° = 30°.
In the right-angled $\triangle$ADC, $\angle$CAD = 90° - $\angle$C = 90° - 45° = 45°.
Steps of Construction:
Step 1: Draw a long line $l$. Take any point D on it.

Step 2: At D, construct a perpendicular line DX to $l$.

Step 3: From the ray DX, cut off a line segment DA of length 4.5 cm. This fixes the vertex A.
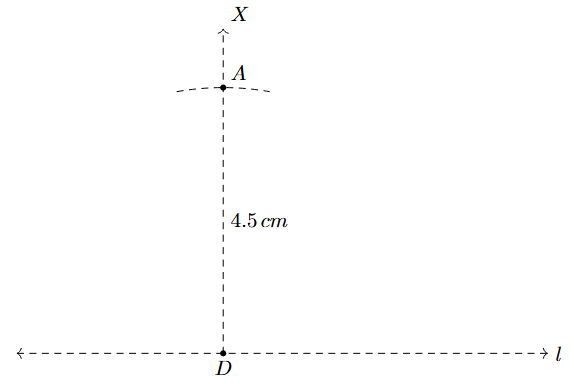
Step 4: Now, at vertex A, construct an angle $\angle$DAB = 30° (since 90°-60° = 30°). Let the ray AB intersect the line $l$ at point B.

Step 5: On the other side of AD, at vertex A, construct an angle $\angle$DAC = 45° (since 90°-45° = 45°). Let the ray AC intersect the line $l$ at point C.
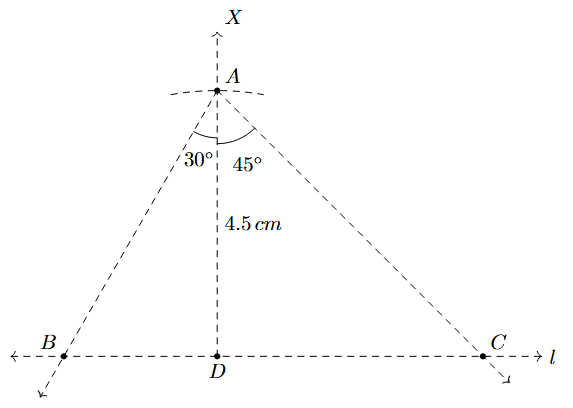
Step 6: The triangle ABC is the required triangle with altitude AD = 4.5 cm, $\angle$B = 60°, and $\angle$C = 45°.
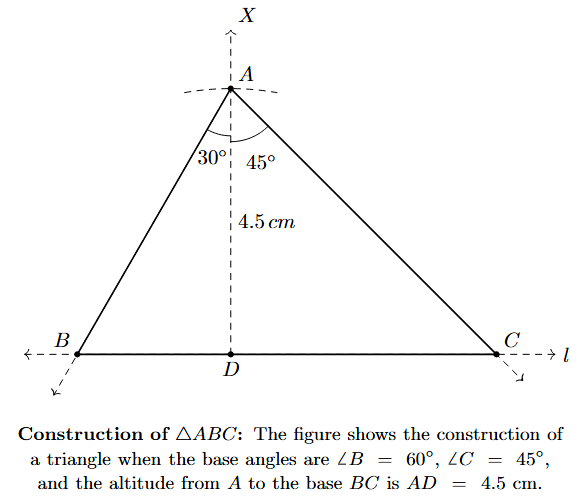
Justification:
We need to justify that the constructed triangle ABC has the given angles and altitude.
To Prove:
In the constructed $\triangle \text{ABC}$, the altitude AD = 4.5 cm, $\angle \text{ABC} = 60^\circ$, and $\angle \text{ACB} = 45^\circ$.
Proof:
By construction (Step 3), the length of AD is 4.5 cm. By construction (Step 2), AD is perpendicular to the line $l$ which contains the base BC. Therefore, AD is the altitude from A to BC, and its length is 4.5 cm.
Now, consider the right-angled triangle $\triangle \text{ADB}$.
The sum of angles in a triangle is $180^\circ$.
$\angle \text{BAD} + \angle \text{ABD} + \angle \text{ADB} = 180^\circ$
We know $\angle \text{ADB} = 90^\circ$ and by construction, $\angle \text{BAD} = 30^\circ$.
$30^\circ + \angle \text{ABD} + 90^\circ = 180^\circ$
$\angle \text{ABD} = 180^\circ - 90^\circ - 30^\circ$
$\angle \text{ABD} = 60^\circ$
So, the angle $\angle$B of the triangle is 60°, which matches the given condition.
Similarly, consider the right-angled triangle $\triangle \text{ADC}$.
$\angle \text{CAD} + \angle \text{ACD} + \angle \text{ADC} = 180^\circ$
We know $\angle \text{ADC} = 90^\circ$ and by construction, $\angle \text{CAD} = 45^\circ$.
$45^\circ + \angle \text{ACD} + 90^\circ = 180^\circ$
$\angle \text{ACD} = 180^\circ - 90^\circ - 45^\circ$
$\angle \text{ACD} = 45^\circ$
So, the angle $\angle$C of the triangle is 45°, which matches the given condition.
Since all given conditions (altitude and two base angles) are met, the construction is justified.
Construction of a Right Angled Triangle when Hypotenuse and Length of one Side is Given
In this construction, we are given the lengths of the hypotenuse and one of the other two sides (legs) of a right-angled triangle. We need to construct the triangle using a compass and straightedge.
Let the given right-angled triangle be $\triangle \text{ABC}$, with the right angle at B ($\angle \text{B} = 90^\circ$). Let the length of the hypotenuse AC be $h$ and the length of one side, say AB, be $s$. We need to construct $\triangle \text{ABC}$ given $h$ and $s$.
Note: For a right-angled triangle to be constructible with a given hypotenuse and one side, the length of the side must be less than the length of the hypotenuse ($s < h$). If $s \ge h$, the construction would not be possible.
Construction: To construct a right-angled triangle given its hypotenuse and one side.
This construction is based on the Pythagorean theorem and is a direct application of the Side-Angle-Side (SAS) principle once the right angle is established. We start by drawing the given side, constructing the right angle at one of its endpoints, and then using the hypotenuse length to locate the third vertex.
General Steps of Construction:
- Draw a line segment equal to the length of the given side (leg).
- At one endpoint of this segment, construct a perpendicular line (a 90° angle).
- From the other endpoint of the segment, draw an arc with a radius equal to the length of the hypotenuse.
- The point where this arc intersects the perpendicular line is the third vertex of the triangle. Join the vertices to complete the triangle.
Example. Construct a right-angled triangle ABC, where the right angle is at B, the side AB = 3 cm, and the hypotenuse AC = 5 cm.
Answer:
Given:
- A right-angled triangle ABC with $\angle$B = 90°.
- Length of side AB = 3 cm.
- Length of hypotenuse AC = 5 cm.
To Construct:
The right-angled triangle ABC.
Steps of Construction:
Step 1: Draw a line segment AB of length 3 cm.

Step 2: At point B, construct a ray BX perpendicular to AB, so that $\angle$ABX = 90°.

Step 3: With A as the centre and a radius of 5 cm (the length of the hypotenuse), draw an arc to intersect the ray BX. Mark the point of intersection as C.

Step 4: Join A to C. The triangle ABC is the required right-angled triangle.

Justification:
We need to justify that the constructed triangle ABC is a right-angled triangle with the given side and hypotenuse lengths.
To Prove:
$\triangle \text{ABC}$ is a right-angled triangle with $\angle \text{B} = 90^\circ$, side $\text{AB}$ has the given length, and hypotenuse $\text{AC}$ has the given length.
Proof:
By construction (Step 1), the length of the line segment AB is equal to the given side length.
AB = given side length
(By construction)
By construction (Step 2), the ray BX is perpendicular to AB at point B. Since C lies on BX, the angle $\angle \text{ABC}$ is $90^\circ$.
$\angle \text{ABC} = 90^\circ$
(By construction)
Since one angle of $\triangle \text{ABC}$ is $90^\circ$, it is a right-angled triangle.
The side opposite the right angle is the hypotenuse. Here, the side opposite $\angle$B is AC.
By construction (Step 3), point C lies on the arc drawn with centre A and radius equal to the given hypotenuse length. Therefore, the distance from A to C is equal to the given hypotenuse length.
AC = given hypotenuse length
(By construction)
Thus, we have constructed a triangle ABC which is right-angled at B, has the given side length AB, and the given hypotenuse length AC. The construction is justified.
Note: This construction is only possible if the hypotenuse is longer than the given side (hypotenuse > leg). If the hypotenuse were shorter or equal, the arc from A would not intersect the perpendicular ray BX at a distinct point from B, and a triangle could not be formed. This is consistent with the Pythagorean theorem.
Construction of an Isosceles Triangle
An isosceles triangle is a triangle that has at least two sides of equal length. The third side is called the base. The angles opposite the equal sides are called base angles, and they are also equal. The angle included between the two equal sides is called the vertex angle. We can construct an isosceles triangle given specific information, such as the length of the base and the length of the two equal sides.
Construction: To construct an isosceles triangle given the length of the base and the length of the equal sides.
An isosceles triangle is a triangle that has two sides of equal length. The construction is based on the SSS (Side-Side-Side) criterion. For a triangle to be constructible with side lengths $b, a, a$, the triangle inequality must hold. This means the sum of any two sides must be greater than the third side. The condition is $a + a > b$, or simply $2a > b$. (The other condition, $a + b > a$, is always true since $b > 0$).
General Steps of Construction:
- Draw a line segment equal to the length of the given base.
- From one endpoint of the base, draw an arc with a radius equal to the length of the equal sides.
- From the other endpoint of the base, draw a second arc with the same radius, intersecting the first arc.
- The point of intersection is the third vertex of the triangle. Join this vertex to the endpoints of the base.
Example. Construct an isosceles triangle PQR where the base QR = 5 cm and the length of the equal sides PQ and PR is 6 cm.
Answer:
Given:
- Base QR = 5 cm.
- Length of equal sides PQ = PR = 6 cm.
To Construct:
An isosceles triangle PQR with the given measurements.
Steps of Construction:
Step 1: Draw a line segment QR of length 5 cm. This will be the base of the triangle.

Step 2: With Q as the centre, draw an arc with a radius of 6 cm.

Step 3: With R as the centre and the same radius of 6 cm, draw another arc to intersect the arc from Step 2. Mark the point of intersection as P.

Step 4: Join PQ and PR. The triangle PQR is the required isosceles triangle.

Justification:
We need to justify that the triangle PQR constructed is an isosceles triangle with the given base and equal side lengths.
To Prove:
$\triangle \text{PQR}$ is an isosceles triangle with base QR = 5 cm and equal sides PQ = PR = 6 cm.
Proof:

By construction (Step 1), the length of the base is:
QR = 5 cm
(By construction)
In Step 2, we drew an arc with centre Q and radius 6 cm. Since point P lies on this arc, its distance from Q is 6 cm.
PQ = 6 cm
(Radius of the arc from Q)
In Step 3, we drew an arc with centre R and radius 6 cm. Since point P also lies on this arc, its distance from R is 6 cm.
PR = 6 cm
(Radius of the arc from R)
From the above, we have PQ = 6 cm and PR = 6 cm, which means:
PQ = PR
Since the triangle PQR has two sides of equal length, it is an isosceles triangle. All the given conditions are met. Thus, the construction is justified.
Note on other construction cases for Isosceles Triangles:
An isosceles triangle can also be constructed if other sets of information are provided:
- Base and a Base Angle: Construct the base. Construct the given base angle at both endpoints of the base. The intersection of the two rays will be the third vertex.
- An Equal Side and the Vertex Angle: Construct a line segment equal to the side length. At one endpoint, construct the vertex angle. Mark a point on the second ray of this angle at a distance equal to the side length. Join the two endpoints to form the base.
- The Base and the Altitude to the Base: Construct the base. Draw the perpendicular bisector of the base. Mark the third vertex on the perpendicular bisector at a height equal to the given altitude. Join this vertex to the endpoints of the base.
Construction of a Triangle where One Side, One Angle and Sum of Other Two Sides are Provided
In this construction, we are given the length of one side of a triangle, the measure of an angle adjacent to that side (a base angle), and the sum of the lengths of the other two sides. We need to construct the triangle using a compass and straightedge.
Let the given side be BC, its length be $a$. Let the given base angle be $\angle \text{B}$. Let the sum of the other two sides, AB + AC, be $s$. We need to construct $\triangle \text{ABC}$ such that $\text{BC} = a$, $\angle \text{ABC} = \angle \text{B}$, and $\text{AB} + \text{AC} = s$.
Note: For such a triangle to be constructible, the sum of the other two sides must be greater than the given side ($s > a$), and the given angle $\angle \text{B}$ must be less than $180^\circ$.
Construction: To construct a triangle given its base, a base angle, and the sum of the other two sides.
This construction method involves creating a temporary line segment equal to the sum of the two unknown sides. By forming an isosceles triangle within the construction, we can locate the third vertex of the required triangle. The key principle is using a perpendicular bisector to find a point that is equidistant from two other points.
General Steps of Construction:
- Draw the base of the triangle (e.g., BC) with the given length.
- At one endpoint of the base (B), construct the given base angle ($\angle$B). Draw a long ray (BX).
- From this ray (BX), cut a line segment (BD) equal in length to the given sum of the other two sides (AB + AC).
- Join the point D to the other endpoint of the base (C). This forms a triangle BDC.
- Construct the perpendicular bisector of the segment DC.
- The point where the perpendicular bisector intersects the long ray BD is the third vertex of the required triangle (A).
- Join this vertex (A) to the endpoint of the base (C) to complete the triangle ABC.
Example. Construct a triangle ABC in which the base BC = 7 cm, the base angle $\angle$B = 75°, and the sum of the other two sides AB + AC = 13 cm.
Answer:
Given:
- Base BC = 7 cm.
- Base angle $\angle$B = 75°.
- Sum of sides AB + AC = 13 cm.
To Construct:
A triangle ABC with the given measurements.
Steps of Construction:
Step 1: Draw a line segment BC of length 7 cm.

Step 2: At point B, construct a ray BX such that $\angle \text{XBC} = 75^\circ$.

Step 3: From the ray BX, cut off a line segment BD of length 13 cm (equal to AB + AC).
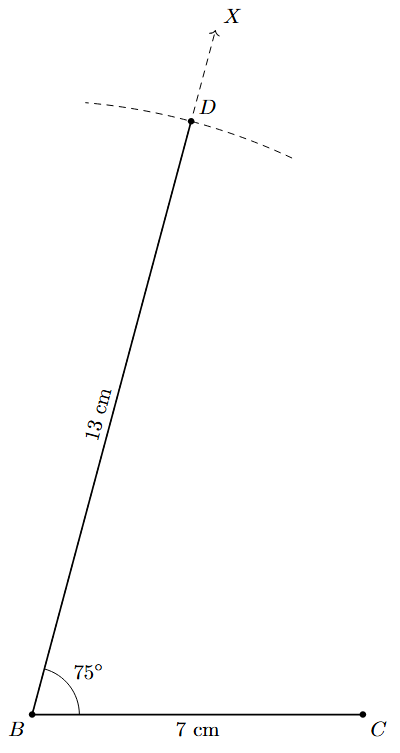
Step 4: Join D to C to form the line segment DC.

Step 5: Construct the perpendicular bisector of the line segment DC. Let this bisector intersect BD at point A.

Step 6: Join A to C. The triangle ABC is the required triangle.

Justification:
We need to justify that the constructed triangle ABC satisfies all the given conditions.
To Prove:
In $\triangle \text{ABC}$, BC has the given length, $\angle \text{ABC}$ is the given angle, and the sum of sides AB + AC is equal to the given sum.
Proof:
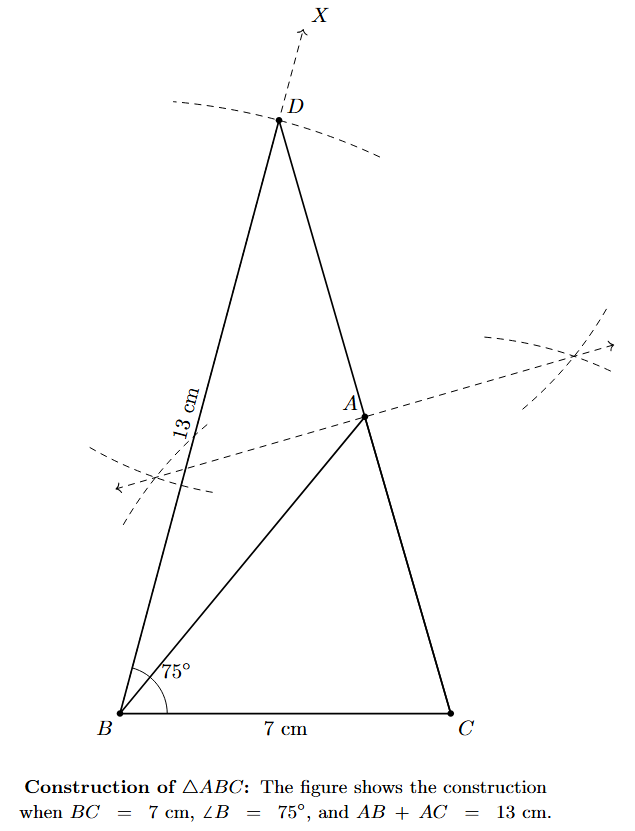
By construction, the base BC has the given length and the angle $\angle \text{ABC}$ is the given angle, as A lies on the ray BX.
Point A lies on the perpendicular bisector of the line segment DC. A key property of a perpendicular bisector is that any point on it is equidistant from the endpoints of the segment.
Therefore,
AC = AD
(A is on the perpendicular bisector of DC)
Now, consider the segment BD. Point A lies on BD. So, we can write:
BD = AB + AD
(Point A lies on segment BD)
By substituting AC for AD in the above equation, we get:
BD = AB + AC
From our construction (Step 3), we know that we cut BD to be equal to the given sum of the sides.
BD = given sum (AB + AC)
(By construction)
Therefore,
AB + AC = given sum
Thus, the constructed triangle ABC has the given base BC, the given base angle $\angle$B, and the sum of the other two sides AB + AC is equal to the given sum. The construction is justified.
Construction of a Triangle where One Side, One Angle and Difference of Other Two Sides are Provided
In this construction, we are given the length of one side of a triangle, the measure of an angle adjacent to that side (a base angle), and the absolute difference of the lengths of the other two sides. This construction has two cases, depending on which of the other two sides is longer.
Let the given side be BC, its length be $a$. Let the given base angle be $\angle \text{B}$. Let the given difference of the other two sides be $d = |\text{AB} - \text{AC}|$. We need to construct $\triangle \text{ABC}$ such that $\text{BC} = a$, $\angle \text{ABC} = \angle \text{B}$, and $|\text{AB} - \text{AC}| = d$.
Note: For a triangle to be constructible, the difference of any two sides must be less than the third side. In this case, $|\text{AB} - \text{AC}| < \text{BC}$, so $d < a$. If $d \ge a$, the construction is not possible. Also, the given angle $\angle \text{B}$ must be less than $180^\circ$.
Construction: To construct a triangle given its base, a base angle, and the difference of the other two sides.
This construction method has two distinct cases, depending on which of the two unknown sides is longer. The core idea for both cases is to use the given difference to mark a point on the ray of the base angle (or its extension) and then use a perpendicular bisector to find the third vertex.
Case 1: When the side adjacent to the given angle is longer.
In this case, we are given the base BC, the angle $\angle$B, and the difference AB - AC, where AB > AC.
Example 1. Construct a triangle ABC in which the base BC = 8 cm, the base angle $\angle$B = 45°, and the difference of the other two sides is AB - AC = 3.5 cm.
Answer:
Given:
- Base BC = 8 cm.
- Base angle $\angle$B = 45°.
- Difference of sides AB - AC = 3.5 cm.
To Construct:
A triangle ABC with the given measurements.
Steps of Construction:
Step 1: Draw the base line segment BC of length 8 cm.

Step 2: At point B, construct a ray BX making an angle of 45° with BC (i.e., $\angle$XBC = 45°).

Step 3: From the ray BX, cut off a line segment BD of length 3.5 cm (equal to the given difference AB - AC).

Step 4: Join D to C.

Step 5: Construct the perpendicular bisector of the line segment DC. Let this bisector intersect the ray BX at a point A.

Step 6: Join A to C. The triangle ABC is the required triangle.

Justification (Case 1)
To Prove:
In the constructed $\triangle \text{ABC}$, BC = 8 cm, $\angle \text{ABC} = 45^\circ$, and AB - AC = 3.5 cm.
Proof:
By construction, the base BC = 8 cm and $\angle \text{ABC} = 45^\circ$ as vertex A lies on the ray BX.
Point A lies on the perpendicular bisector of the segment DC. A fundamental property of a perpendicular bisector is that any point on it is equidistant from the endpoints of the segment.
Therefore,
AC = AD
(A is on the perpendicular bisector of DC)
Now, consider the ray BX. Point D lies on the segment AB. So, we can write:
AB = AD + DB
Rearranging this gives:
DB = AB - AD
By substituting AC for AD (since AC = AD), we get:
DB = AB - AC
From our construction (Step 3), we set the length of DB to be 3.5 cm.
DB = 3.5 cm
(By construction)
Therefore,
AB - AC = 3.5 cm
Thus, the constructed triangle ABC meets all the given conditions. The construction is justified.
Case 2: When the side opposite the given angle is longer.
In this case, we are given the base BC, the angle $\angle$B, and the difference AC - AB, where AC > AB.
Example 2. Construct a triangle ABC in which the base BC = 6 cm, the base angle $\angle$B = 60°, and the difference of the other two sides is AC - AB = 2 cm.
Answer:
Given:
- Base BC = 6 cm.
- Base angle $\angle$B = 60°.
- Difference of sides AC - AB = 2 cm.
To Construct:
A triangle ABC with the given measurements.
Steps of Construction:
Step 1: Draw the base line segment BC of length 6 cm.

Step 2: At point B, construct a ray BX making an angle of 60° with BC.

Step 3: Extend the ray BX downwards to a point Y. From this extended ray BY, cut off a line segment BD of length 2 cm (equal to AC - AB).

Step 4: Join D to C.

Step 5: Construct the perpendicular bisector of the line segment DC. Let this bisector intersect the original ray BX at a point A.

Step 6: Join A to C. The triangle ABC is the required triangle.

Justification (Case 2)
To Prove:
In the constructed $\triangle \text{ABC}$, BC = 6 cm, $\angle \text{ABC} = 60^\circ$, and AC - AB = 2 cm.
Proof:
By construction, the base BC = 6 cm and $\angle \text{ABC} = 60^\circ$ as vertex A lies on the original ray BX.
Point A lies on the perpendicular bisector of the segment DC. Therefore, point A is equidistant from points D and C.
AC = AD
(A is on the perpendicular bisector of DC)
Now, consider the line YX. Point B lies on the segment AD. So, we can write:
AD = AB + BD
By substituting AC for AD (since AC = AD), we get:
AC = AB + BD
Rearranging this gives:
AC - AB = BD
From our construction (Step 3), we set the length of BD to be 2 cm.
BD = 2 cm
(By construction)
Therefore,
AC - AB = 2 cm
Thus, the constructed triangle ABC meets all the given conditions. The construction is justified.
Construction of a Triangle where Two Angles and Sum of all the Three Sides are Provided
In this construction, we are given the measures of two base angles of a triangle and the sum of the lengths of all three sides (perimeter). We need to construct the triangle using a compass and straightedge.
Let the given base angles be $\angle \text{B}$ and $\angle \text{C}$. Let the given perimeter (sum of sides AB + BC + CA) be $P$. We need to construct $\triangle \text{ABC}$ such that $\angle \text{ABC} = \angle \text{B}$, $\angle \text{ACB} = \angle \text{C}$, and $\text{AB} + \text{BC} + \text{CA} = P$.
Note: For a triangle to be constructible with given angles $\angle \text{B}$ and $\angle \text{C}$, the sum of these angles must be less than $180^\circ$ ($\angle \text{B} + \angle \text{C} < 180^\circ$).
Construction: To construct a triangle given its perimeter and two base angles.
This is a complex construction that cleverly uses the properties of isosceles triangles and perpendicular bisectors. The main idea is to first draw a line segment equal to the perimeter. Then, by creating specific angles at the endpoints of this segment and using bisectors, we can locate the apex of the triangle. The base vertices are then found by constructing perpendicular bisectors.
General Steps of Construction:
- Draw a line segment (e.g., PQ) equal in length to the given perimeter.
- At the endpoints of this segment (P and Q), construct angles equal to the given base angles (e.g., $\angle$B and $\angle$C).
- Bisect these two angles. The point where the angle bisectors intersect is the apex of the required triangle (A).
- Construct the perpendicular bisector of the segment connecting the apex to one endpoint of the perimeter line (AP). The intersection of this bisector with the perimeter line gives one base vertex (B).
- Construct the perpendicular bisector of the segment connecting the apex to the other endpoint of the perimeter line (AQ). The intersection of this bisector with the perimeter line gives the other base vertex (C).
- Join the vertices to form the required triangle (ABC).
Example. Construct a triangle ABC in which the base angles are $\angle$B = 60° and $\angle$C = 45°, and the perimeter AB + BC + CA = 11 cm.
Answer:
Given:
- Base angle $\angle$B = 60°.
- Base angle $\angle$C = 45°.
- Perimeter (AB + BC + CA) = 11 cm.
To Construct:
A triangle ABC with the given measurements.
Steps of Construction:
Step 1: Draw a line segment PQ of length 11 cm.

Step 2: At point P, construct a ray PX such that $\angle \text{XPQ} = 60^\circ$ (equal to $\angle$B).

Step 3: At point Q, construct a ray QY such that $\angle \text{YQP} = 45^\circ$ (equal to $\angle$C).

Step 4: Construct the bisectors of $\angle$XPQ and $\angle$YQP. Let these bisectors intersect at a point A.

Step 5: Construct the perpendicular bisector of the line segment AP. Let it intersect PQ at point B.

Step 6: Construct the perpendicular bisector of the line segment AQ. Let it intersect PQ at point C.

Step 7: Join AB and AC. The triangle ABC is the required triangle.

Justification:
To Prove:
In the constructed $\triangle \text{ABC}$, the perimeter AB + BC + CA = 11 cm, $\angle \text{ABC} = 60^\circ$, and $\angle \text{ACB} = 45^\circ$.
Proof:
1. Proof of Perimeter:
Point B lies on the perpendicular bisector of the segment AP. Any point on the perpendicular bisector is equidistant from the endpoints of the segment.
AB = PB
... (i)
Similarly, point C lies on the perpendicular bisector of the segment AQ.
AC = QC
... (ii)
The segment PQ is made up of PB, BC, and QC.
PQ = PB + BC + QC
Substituting from (i) and (ii), we get:
PQ = AB + BC + AC
By construction, PQ = 11 cm. Therefore, the perimeter of $\triangle$ABC is 11 cm.
2. Proof of Angles:
Consider $\triangle$APB. Since AB = PB (from (i)), it is an isosceles triangle. The angles opposite the equal sides are equal.
$\angle \text{BAP} = \angle \text{BPA}$
The angle $\angle$ABC is an exterior angle to $\triangle$APB. The exterior angle is the sum of the two interior opposite angles.
$\angle \text{ABC} = \angle \text{BAP} + \angle \text{BPA}$
Since $\angle \text{BAP} = \angle \text{BPA}$, we can write:
$\angle \text{ABC} = 2 \times \angle \text{BPA}$
By construction, the angle $\angle$XPQ was made equal to 60°, and the ray PA is its bisector. Therefore:
$\angle \text{BPA} = \angle \text{QPA} = \frac{1}{2} \angle \text{XPQ} = \frac{1}{2} \times 60^\circ = 30^\circ$
So, $\angle \text{ABC} = 2 \times 30^\circ = 60^\circ$. This matches the given angle $\angle$B.
Similarly, consider $\triangle$AQC. Since AC = QC (from (ii)), it is an isosceles triangle.
$\angle \text{CAQ} = \angle \text{CQA}$
The angle $\angle$ACB is an exterior angle to $\triangle$AQC.
$\angle \text{ACB} = \angle \text{CAQ} + \angle \text{CQA}$
Since $\angle \text{CAQ} = \angle \text{CQA}$, we can write:
$\angle \text{ACB} = 2 \times \angle \text{CQA}$
By construction, the angle $\angle$YQP was made equal to 45°, and the ray QA is its bisector. Therefore:
$\angle \text{CQA} = \angle \text{PQA} = \frac{1}{2} \angle \text{YQP} = \frac{1}{2} \times 45^\circ = 22.5^\circ$
So, $\angle \text{ACB} = 2 \times 22.5^\circ = 45^\circ$. This matches the given angle $\angle$C.
Thus, the constructed triangle ABC has the given perimeter and the given base angles. The construction is justified.

